Group of rational points on the unit circle

In mathematics, the rational points on the unit circle are those points (x, y) such that both x and y are rational numbers (fractions) and satisfy x2 + y2 = 1. The set of such points turns out to be closely related to primitive Pythagorean triples. Consider a primitive right triangle, that is, with integral side lengths a, b, c, with c the hypotenuse, such that the sides have no common factor larger than 1. Then on the unit circle there exists the rational point (a/c, b/c). Conversely, if (x, y) is a rational point on the unit circle, then there exists a primitive right triangle with sides xc, yc, c.

Contents

Group operation

The set of rational points forms an infinite abelian group, which shall be called G in this article. The identity element is the point (1, 0). The group operation, or "sum" is (x, y) + (t, u) = (xt − uy, xu + yt). This is angle addition since x = cos(A) and y = sin(A), where A is the angle the radius vector (x, y) makes with the radius vector (1,0), measured counter clockwise. So with (x, y) and (t, u) forming angles A and B, respectively, with (1, 0), their sum (xt − uy, xu + yt) is just the rational point on the unit circle with angle A + B (ordinary sum).

Example

The points on the unit circle: (3/5,4/5) and (5/13,12/13) [corresponding to the two most famous Pythagorean right triangles:3,4,5 and 5,12,13] are elements of G, and their group product is (-33/65,56/65), which corresponds to a 33,56,65 Pythagorean right triangle. Notice that the sum of the squares of 33 and 56 is the square of 65.

Group structure

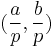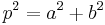The structure of G is an infinite sum of cyclic groups. If C4 denotes the cyclic subgroup with four elements generated by the point (0, 1), and Z is any infinite cyclic subgroup generated by a point of form (\frac{a}{p}, \frac{b}{p}) where p^2 = a^2 %2B b^2 is the square of a prime of form 4k + 1, (and a, b are positive) then G is isomorphic to C4 ⊕ Z ⊕ Z ⊕ ..., going on forever. Since it is an direct sum rather than direct product, only finitely many of the values in the Zs differ from zero.

See also

References